Метод быстрой фильтрации потока данных о глобальной позиции наблюдаемого объекта на примере GPS-телеметрии
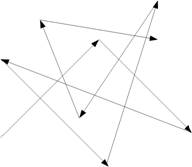
Рис.1. Пример шума в GPS-телеметрии с неподвижного объекта
В сложных системах мониторинга по сбору и хранению GPS-телеметрии от множества объектов, использование фильтрации позволяет значительно сократить объёмы обрабатываемой информации без потери качества последней, т.о. задача фильтрации заключается в отсеве данных, не дающих принципиально новой информации о положении объекта. Важно отметить, что фильтрацию в подобных системах разумно реализовывать на источнике данных, это значительно снизит нагрузку на канал передачи данных и сервер, позволит реализовать передачу данных в режиме стека (приоритет за новыми данными), такой подход требует со стороны алгоритма минимум вычислений, посильный для большинства микроконтроллеров.
Предложенный фильтр GPS-телеметрии можно разделить на две части: предварительный фильтр и фильтр избыточных данных. Общая схема фильтра изображена на рисунке 2.
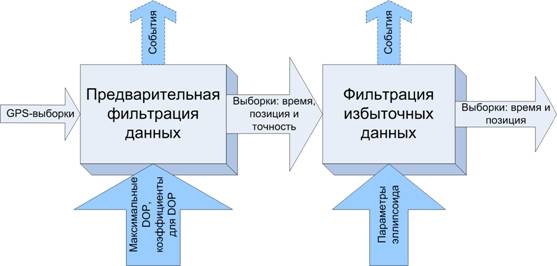
Рис.2. Общая схема фильтра
В схеме фильтра, GPS-выборкой обозначен необходимый набор данных, формируемый GPS-приемником (далее просто выборка, в географическом смысле – позиция или точка, рис. 3):
- $Т$ – время по Гринвичу (от 1970 года)
- $\varphi$ – широта в градусах (от -90 до 90, положительное значение примем в соответствие северному полушарию)
- $\lambda$ – долгота в градусах (от -180 до 180, положительное значение примем в соответствие восточному полушарию)
- $h$ – эллипсоидная высота в метрах (может иметь отрицательное значение)
- $PDOP$ – позиционный фактор потери точности (в пространстве)
- $VDOP$ – вертикальный фактор потери точности (только по высоте)
- $HDOP$ – горизонтальный фактор потери точности (на плоскости касательной к рассматриваемой точке поверхности эллипсоида)
- $M$ – режим определения местоположения [1] (учитывая разнообразность протоколов и различный подход к формированию данного параметра, обозначим это как набор состояний: 0 – Сигнал GPS отсутствует, 1 – Доступно только время, 2 - Двухмерный режим позиционирования, 3 - Трехмерный режим позиционирования)
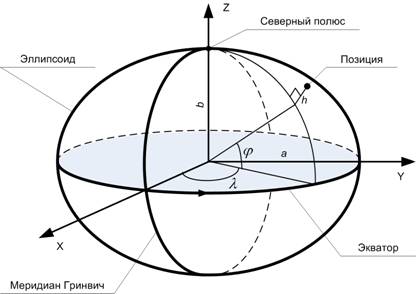
Рис.3. Иллюстрация системы координат и параметров эллипсоида
Предварительная фильтрация реализует отсев выборок, которые являются ошибочными, неполными или не соответствуют режиму, для этого анализируется $M$. Для ряда приложений на данном этапе фильтрации может оказаться полезным, предусмотреть генерацию таких событий, как «потеря сигнала GPS» и «начало работы фильтра». Дополнительно, в зависимости от требований к качеству данных, можно отсеивать выборки, в которых значения $DOP$ выходят за максимально допустимые пределы, указанные в настройках фильтра. Для $HDOP$ рекомендуется брать максимально допустимое значение $HDOPmax$ равным $3...6$, для $VDOP – VDOPmax=4...7$. Максимально допустимый $PDOP$ ($PDOPmax$) можно взять, исходя из того, что все три рассматриваемых DOP связаны отношением: $PDOP=\sqrt{{VDOP}^{2}+{HDOP}^{2}}$ [2].
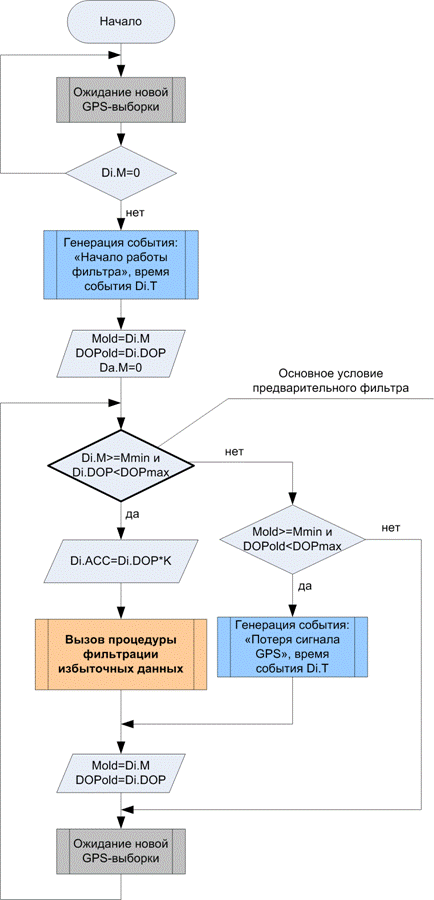
Рис.4. Алгоритм предварительной фильтрации
Алгоритм предварительной стадии фильтрации, изображен на рисунке 4. При старте предложенный алгоритм проверяет поступающие GPS-выборки ($Di$) до тех пор, пока GPS-сигнал отсутствует ($M=0$), для генерации события «начала работы фильтра», затем инициализируются вспомогательные переменные, и начинается основной цикл фильтрации. Для случая, когда достаточно двух координат – широты и долготы, $Mmin$ берется равным 2 (Двухмерный режим позиционирования), а в качестве $DOP$ и $DOPmax$ используем горизонтальный фактор потери точности $HDOP$ и $HDOPmax$. Для трехмерного случая $Mmin$ = 3 (Трехмерный режим позиционирования), а в качестве $DOP$ и $DOPmax$ используем позиционный фактор потери точности $PDOP$ и $PDOPmax$. Переменные $Mold$ и $DOPold$ служат для хранения значений $M$ и $DOP$ из предшествующей GPS-выборки. Если основное условие выполняется, то при подготовке данных для следующего этапа фильтрации вычисляется значение точности позиционирования ($ACC$) в метрах. В случае если основное условие не выполнилось, а предшествующая выборка удовлетворяла данному условию, формируется событие «потери GPS-сигнала».
Точность позиционирования ($ACC$) необходима для анализа данных на предмет их избыточности. Аналогично $DOP$ можно выделить 3 типа точности позиционирования:
- $PACC$ – позиционная точность (в пространстве) в метрах
- $VACC$ – вертикальная точность (только по высоте) в метрах
- $HACC$ – горизонтальная точность (на плоскости касательной к рассматриваемой точке поверхности эллипсоида) в метрах
Известно, что $PACC$, $VACC$ и $HACC$ зависят от псевдо диапазона измерений и прямо пропорциональны значениям $PDOP$, $VDOP$ и $HDOP$ соответственно [3]. Поскольку точность позиционирования никак не определяется из GPS-выборки, для получения значений $PACC$, $VACC$ и $HACC$ необходимо экспериментальным путем подобрать коэффициенты к соответствующим значениям $PDOP$, $VDOP$ и $HDOP$, т.е.
$$PACC=PDOP \cdot KP \\ VACC=VDOP \cdot KV \\ HACC=HDOP \cdot KH$$
где $KP$, $KV$ и $KH$ – соответствующие коэффициенты для $DOP$ в метрах, далее просто коэффициенты, они указываются в настройках грубого фильтра – рисунок 2.
Рекомендовать строго определенные коэффициенты нельзя, поскольку точность позиционирования зависит не только от качества сигналов со спутников, но так же от типа приемника. Диапазон рекомендуемых значений следующий: 3...5 метров для $HDOP$, 3...6 метров для $VDOP$ и 3...5 метров для $PDOP$.
Фильтр избыточных данных в качестве критерия использует расстояние между двумя точками, которое не должно быть меньше суммы их точностей позиционирования. Графически это представлено на рисунке 5, радиус окружности (сферы в трёхмерном случае) берётся равным значению точности ($ACC$) для данной точки. Новые выборки проходят фильтрацию при условии, что их окружность не пересекается с окружностью предыдущей прошедшей фильтрацию выборки. Если фильтрацию подобного типа не выполнять, то помимо лишних, не несущих полезной информации данных, будет наблюдаться шум, пример которого изображен на рисунке 1.
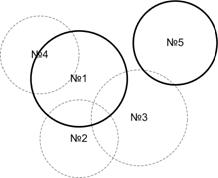
Рис.5. Иллюстрация к алгоритму фильтрации избыточных данных о позиции наблюдаемого объекта
Для вычисления расстояния ($L$) между двумя позициями на эллипсоиде необходимо использовать формулы [3] перевода эллипсоидных координат в декартовы и расстояния между двумя точками:
$$x = \left[ \frac{a}{\sqrt{ 1-\frac{{a}^{2}-{b}^{2}}{{a}^{2}} \cdot {\sin}^2 (\varphi) }}+h \right] \cdot \cos (\varphi) \cdot \cos (\lambda) \text{, (1)} \\
y = \left[ \frac{a}{\sqrt{ 1-\frac{{a}^{2}-{b}^{2}}{{a}^{2}} \cdot {\sin}^2 (\varphi) }}+h \right] \cdot \cos (\varphi) \cdot \sin (\lambda) \text{, (2)} \\
z = \left[ \frac{a}{\sqrt{ 1-\frac{{a}^{2}-{b}^{2}}{{a}^{2}} \cdot {\sin}^2 (\varphi) }} \cdot \left[ 1-\frac{{a}^{2}-{b}^{2}}{{a}^{2}} \right] +h \right] \cdot \sin (\varphi) \text{, (3)} \\
L = \sqrt{({{x}_{a}-{x}_{i})}^2+{({y}_{a}-{y}_{i})}^2+{({z}_{a}-{z}_{i})}^2} \text{, (4)}
$$
где, $a$ и $b$ являются параметрами эллипсоида, используемого в мировой геодезической системе отсчета WGS-84, используемой в GPS:
- $a = 6378137.00$ м. – большая полуось
- $b = 6356752.31$ м. – малая полуось
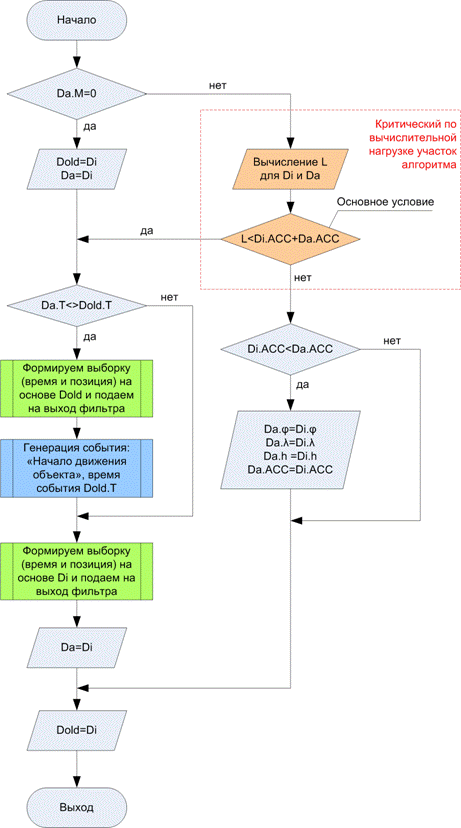
Рис.6. Алгоритм фильтрации избыточных данных
Алгоритм фильтрации избыточных данных приведен на рисунке 6. $Da$ – это последняя выборка, которая удовлетворила основному условию данного фильтра. Если фильтр только начал свою работу, т.е. $Da.M=0$, то $Di$ – текущая выборка, прошедшая предварительный фильтр, копируется в $Dold$ и $Da$, после чего фильтр выдает первую выборку на основе $Di$. $Dold$ обозначена копия предшествующей выборки, поступившей на вход рассматриваемого фильтра.
В рабочем режиме ($Da.M<>0$) вычисляется расстояние ($L$) между выборками $Di$ и $Da$, затем проверяется основное условие фильтра на избыточность данных. Если основное условие выполнено, т.е. выборка $Di$ не является избыточной, переходим к формированию выходных выборок (время, позиция) и сообщений. Прежде чем сформировать выборку на основе $Di$, необходимо проверить совпадает ли время $Di$ и $Dold$, т.е. прошла ли фильтрацию предыдущая выборка $Dold$, если нет, на ее основе формируем выходную выборку и событие о «начале движения объекта». Это может понадобиться для дальнейшей обработки выборок, например для более точного вычисления скорости наблюдаемого объекта, подсчета времени его нахождения в подвижном состоянии и других случаев, когда важно точно знать момент начала движения.
Если основное условие фильтра избыточных данных не выполняется, но точность у новой выборки лучше, чем у последней прошедшей фильтрацию ($Di.ACC<Da.ACC$), данные о позиции и значения точности копируются из выборки $Di$ в выборку $Da$, в некоторых случаях это помогает улучшить качество фильтрации. Например, когда по каким-то причинам точность ухудшилась с нескольких метров до нескольких десятков метров, без данного приема новые данные поступят из фильтра только после того, как объект покинет зону радиусом в эту точность, несмотря на то, что точность новых выборок будет значительно лучше. В двухмерном режиме позиционирования в качестве точности ($ACC$) используем горизонтальную точность ($HACC$), а высота ($h$) не используется. В трехмерном режиме используется позиционная точность ($PACC$).
В алгоритме на рисунке 6 есть критический момент, требующий относительно больших вычислительных ресурсов. Формулы 1,2,3 и 4 для вычисления расстояния между двумя точками требуют использования чисел с плавающей запятой двойной точности, что является крайне сложной задачей для большинства недорогих микроконтроллеров.
Для ускорения вычислений необходимо отказаться от перевода координат из эллипсоидной системы в декартову, и проводить фильтрацию в исходной системе координат, но в этом случае не удастся вычислить расстояние между двумя точками. Поэтому, основное условие фильтра избыточных данных примет вид (для двухмерного случая последнее выражение с участием $h$ исключается):
$$ \left\{ \begin{matrix} |Da.\varphi - Di.\varphi| \leq \psi (Da.\varphi) \cdot Da.HACC + \psi (Di.\varphi) \cdot Di.HACC \\
|Da.\lambda - Di.\lambda| \leq \chi (Da.\varphi) \cdot Da.HACC + \chi (Di.\varphi) \cdot Di.HACC \\
|Da.h - Di.h| \leq Da.VACC + Di.VACC \end{matrix} \right.,
$$
$ \psi (\varphi)$ и $ \chi (\varphi)$ в новом подходе используются в качестве параметров эллипсоида (рис. 2).
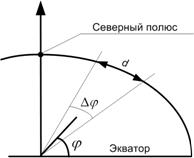
Рис.7. Иллюстрация к функции [tex] \psi (\varphi)[/tex]
$ \psi (\varphi)$ - функция, вычисляющая соотношение градусов широты к одному метру расстояния на указанной в качестве параметра широте. Вычислено, что обратные значения данной функции меняются на протяжении от 0 до 90 градусов широты незначительно, всего на 31 см./сек.Ш. (30,715…31.025 м./сек.Ш.), это значительно меньше максимальной точности позиционирования (2 м.), поэтому $ \psi (\varphi)$ приравнивается константе, равной 1/30.87 = 0,03239391 сек.Ш./м. или $8.9983 \cdot {10}^{-6}$ °Ш./м. на любой широте. Графически смысл единицы измерения (°Ш./м.) можно увидеть на рисунке 7 – это отношение $\frac{\Delta\varphi}{d}$.
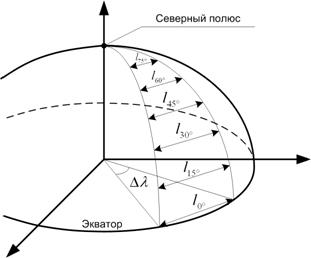
Рис.8. Иллюстрация к функции [tex] \chi (\varphi)[/tex]
$ \chi (\varphi)$ - вычисляет соотношение градусов долготы к одному метру расстояния на указанной широте. Значение данной функции значительно меняется ближе к высоким широтам, в $\pm90°$ переходит в бесконечность, таким образом, данный фильтр нельзя считать надёжным на полюсах, там применение проектируемого устройства маловероятно, но допустимо, если для точек полюсов предусмотреть вместо бесконечности некоторое максимальное значение. Непосредственное вычисление $ \chi (\varphi)$ заменено таблицей, и последующей линейной интерполяцией для промежуточных значений широты, но как показала практика – достаточно таблицы 1 без интерполяции промежуточных данных. Данные для таблицы рассчитаны по формулам 1,2,3,4 в качестве минимального изменения была взята 1 секунда долготы, шаг $j$ по широте равен 1°, в качестве результата в таблицу записаны значения $1/{L}_{j}$. На рисунке 8 значения $ \chi (\varphi)$ можно представить как $\frac{\Delta\lambda}{{l}_{j}}$, очевидно, что оно значительно меняется ближе к высоким широтам.
| Угол по широте | Секунд долготы на метр | Угол по широте | Секунд долготы на метр | Угол по широте | Секунд долготы на метр |
|---|---|---|---|---|---|
| 0 | 0.03233884320 | 30 | 0.03731041962 | 60 | 0.06451511818 |
| 1 | 0.03234373632 | 31 | 0.03769406222 | 61 | 0.06653320062 |
| 2 | 0.03235842324 | 32 | 0.03809740622 | 62 | 0.06870351652 |
| 3 | 0.03238292639 | 33 | 0.03852134593 | 63 | 0.07104288695 |
| 4 | 0.03241728336 | 34 | 0.03896684472 | 64 | 0.07357072470 |
| 5 | 0.03246154695 | 35 | 0.03943494139 | 65 | 0.07630955357 |
| 6 | 0.03251578538 | 36 | 0.03992675665 | 66 | 0.07928565496 |
| 7 | 0.03258008251 | 37 | 0.04044350089 | 67 | 0.08252988653 |
| 8 | 0.03265453828 | 38 | 0.04098648250 | 68 | 0.08607871985 |
| 9 | 0.03273926892 | 39 | 0.04155711734 | 69 | 0.08997557955 |
| 10 | 0.03283440757 | 40 | 0.04215693920 | 70 | 0.09427257874 |
| 11 | 0.03294010455 | 41 | 0.04278761178 | 71 | 0.09903280806 |
| 12 | 0.03305652830 | 42 | 0.04345094207 | 72 | 0.1043333822 |
| 13 | 0.03318386566 | 43 | 0.04414889528 | 73 | 0.1102695673 |
| 14 | 0.03332232296 | 44 | 0.04488361198 | 74 | 0.1169604503 |
| 15 | 0.03347212655 | 45 | 0.04565742741 | 75 | 0.1245568822 |
| 16 | 0.03363352400 | 46 | 0.04647289355 | 76 | 0.1332528193 |
| 17 | 0.03380678488 | 47 | 0.04733280395 | 77 | 0.1433019032 |
| 18 | 0.03399220208 | 48 | 0.04824022254 | 78 | 0.1550423318 |
| 19 | 0.03419009300 | 49 | 0.04919851627 | 79 | 0.1689352890 |
| 20 | 0.03440080090 | 50 | 0.05021139310 | 80 | 0.1856264436 |
| 21 | 0.03462469645 | 51 | 0.05128294539 | 81 | 0.2060484337 |
| 22 | 0.03486217947 | 52 | 0.05241770044 | 82 | 0.2316002322 |
| 23 | 0.03511368070 | 53 | 0.05362067906 | 83 | 0.2644802286 |
| 24 | 0.03537966381 | 54 | 0.05489746403 | 84 | 0.3083524296 |
| 25 | 0.03566062774 | 55 | 0.05625428025 | 85 | 0.3698120485 |
| 26 | 0.03595710914 | 56 | 0.05769808909 | 86 | 0.4620495522 |
| 27 | 0.03626968495 | 57 | 0.05923669971 | 87 | 0.6158426921 |
| 28 | 0.03659897554 | 58 | 0.06087890162 | 88 | 0.9235248195 |
| 29 | 0.03694564797 | 59 | 0.06263462271 | 89 | 1.846762595 |
При расчётах значений $ \psi (\varphi)$ и $ \chi (\varphi)$ $h$ была принята равной 100м., если говорить о точности, то $L$ из расчёта на 1 секунду широты при изменении высоты от 0 до 1000 м. над уровнем эллипсоида изменяется всего на 5 мм, поэтому высотой можно пренебречь для расчёта этих значений.
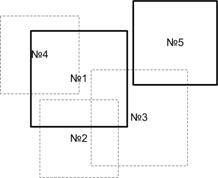
Рис.9. Иллюстрация к быстрому варианту алгоритма фильтрации избыточных данных
Графический смысл алгоритма фильтрации избыточных данных в новом подходе примет вид представленный на рисунке 9. Относительно масштабов, фигуру со сторонами $ 2 \cdot \psi (\varphi) \cdot HACC$ на $ 2 \cdot \chi (\varphi) \cdot HACC$ можно обозначить как прямоугольник, а если задействовать третье измерение ($2 \cdot VACC$), то как параллелепипед. Таким образом, условием принятия новой позиции ($Di$) является не пересечение данных фигур, построенных вокруг точек указанных в выборках $Da$ и $Di$. При таком подходе будет теряться некоторое количество потенциально полезной информации о позиции, если за идеал принять фильтрацию с использованием формул 1-4, графически представленную на рисунке 5. Для движения на плоскости потери можно приблизительно оценить так: $4R^2/\pi R^2 \approx 1.27$, т.е. на 127 отсеянных выборок придется примерно 27 потенциально полезных выборок. Для движения в пространстве: $\frac{8R^3}{\frac{4}{3}\pi R^3} \approx 1.91$, аналогично на 191 отсеянную выборку придется около 91-й потенциально полезной выборки. Подобные потери вполне допустимы, для наблюдения за транспортом. Взамен имеем значительное сокращение вычислений, и возможность использования вычислений с фиксированной запятой, т.о. алгоритм фильтрации становится легко реализуемым и требует минимум вычислительных ресурсов.
В таблице 2 представлены результаты обработки NMEA-трека [1] с использованием разработанных алгоритмов, коэффициенты для $HDOP$ и $VDOP$ были взяты равными 4.5 метра, а для $PDOP$ 3.5 метра. Прочерком в поле «тип фильтра» обозначен результат, полученный без применения фильтрации. Звёздочкой (*) отмечены типы фильтров, в которых использовался быстрый алгоритм. Длительность трека 1 час 33 минуты.
| Тип фильтра | Путь (м.) | Макс. скорость (км/ч) | Число выборок |
|---|---|---|---|
| - | 82627.698 | 92 | 53.5597 |
| 2D | 80328.531 | 90.918 | 1743 |
| 2D* | 80331.885 | 90.918 | 1700 |
| 3D | 80330.503 | 90.918 | 1731 |
| 3D* | 80330.967 | 90.918 | 1695 |
| 2D/3D | 80330.108 | 90.918 | 1733 |
| 2D/3D* | 80331.885 | 90.918 | 1700 |
В таблице 3 приведены результаты обработки 45 минутного NMEA-трека с неподвижного объекта.
| Тип фильтра | Путь (м.) | Макс. скорость (км/ч) | Число выборок |
|---|---|---|---|
| - | 448.856 | 16.294 | 2719 |
| 2D | 0 | 0 | 1 |
| 2D* | 0 | 0 | 1 |
| 3D | 0 | 0 | 1 |
| 3D* | 0 | 0 | 1 |
| 2D/3D | 0 | 0 | 1 |
| 2D/3D* | 0 | 0 | 1 |
Фильтр типа 2D рекомендуется использовать в случае, когда необходимости в 3-й координате нет (не нужно очень точно считать пройденный маршрут или объект практически не передвигается по вертикали – хорошо подходит для морского транспорта и большинства наземного), это позволит уменьшить размер выходной выборки и сократить вычисления.
Трёхмерный режим позиционирования обеспечивается практически всегда, при желании иметь данные в трёх координатах, и не желании усложнять алгоритм можно воспользоваться фильтром 3D типа.
Фильтр типа 2D/3D, построен таким образом, что в предварительной фильтрации (рис. 2) используется двухмерное условие. А при фильтрации избыточных данных, если в обеих выборках ($Di$ и $Da$) $M=3$, то используется трёхмерное условие, иначе двухмерное. Используя данный тип фильтра, в формируемых выборках помимо времени и позиции, необходимо передавать $M$, или просто логическую переменную, определяющую использование высоты. Для таблиц 2 и 3, перед расчётом расстояния между двумя точками (формулы 1,2,3 и 4), проверялось значение $M$ и если хотя бы в одной из выборок режим не соответствовал трехмерному, то вместо высот использовалась константа. Фильтр типа 2D/3D имеет смысл, когда необходимо знать о местоположении объекта как можно больше.
В качестве основных достоинств разработанного метода фильтрации GPS-телеметрии можно отметить: первое – возможность реализации алгоритма на маломощном и недорогом микроконтроллере. Второе – значительное уменьшение потока телеметрии, в зависимости от характера движения наблюдаемого объекта и того, какие коэффициенты выбраны для $DOP$. Третье – улучшается точность вычисления производных параметров (путь, скорость, время движения и др.).
В ходе разработки метода фильтрации было написано специальное программное обеспечение, демонстрирующее работу GPS-модуля, фильтрацию и осуществляющее расчёты для таблиц, приведенных в статье. Скачать программу и получить более подробную информацию можно по адресу в Интернете: «http://altmer.arts-union.ru/GPSTester.htm».
Список литературы
- ANTARIS Positioning Engine - Protocol Specification, Copyright 2003 © u-blox AG
- Richard B. Langley, Dilution of Precision, GPS World 2000. Ссылка на перевод статьи: http://www.navgeocom.ru/gps/dop/
- Jean-Marie Zogg, Основы GPS, 26/03/2002, ID документа: Gps-x-02007-R.pdf
Список терминов
- DOP – Фактор потери точности (англ. Dilution of precision) — термин, использующийся в области систем глобального позиционирования для описания качества геометрического взаиморасположения спутников друг относительно друга.
- GPS – NAVSTAR GPS (англ. Navigation Satellite Time and Ranging, Global Positioning System — Измерение дальности и времени по навигационному спутнику, Глобальная система позиционирования) — спутниковая система навигации, часто именуемая просто GPS. Система разработана, реализована и эксплуатируется Министерством обороны США.
- GPS-телеметрия – Подразумеваются данные с GPS приемника удаленного объекта.
- NMEA – «National Marine Electronics Association» — полное название «NMEA 0183» — текстовой протокол связи морского (как правило, навигационного) оборудования между собой. Стал особенно популярен в связи с распространением GPS приёмников, использующих этот стандарт.
- NMEA-трек – запись данных, сделанная в течении некоторого времени, с устройства, вещающего по протоколу NMEA.
 Проект эмуляции
Проект эмуляции