Метод сегментации сферы при моделировании поверхности планет
Для решения перечисленных задач разработан метод прямой (не рекурсивной) сегментации поверхности сферы, обеспечивающий хорошее качество сегментной сетки при сколь угодно большой глубине (уровне) сегментации. Чтобы метод сегментации был прямым, введена сегментная система координат, которая гарантирует однозначный переход к сферической системе координат и обратно. Данная система координат использует 20 базовых треугольников основанных на икосаэдре [2] (рис.1), образующих 10 базовых сегментов, каждый из которых является локальной системой координат с осями $\bar{x}$ и $\bar{y}$, при сегментации по данным осям пограничные вершины соседних базовых сегментов полностью совпадают, тем самым гарантируется бесшовная визуализация. Важно отметить, что можно интерпретировать входные и выходные сферические координаты как эллипсоидные, но со стороны сегментной системы координат, в ходе преобразований, они воспринимаются именно как сферические.
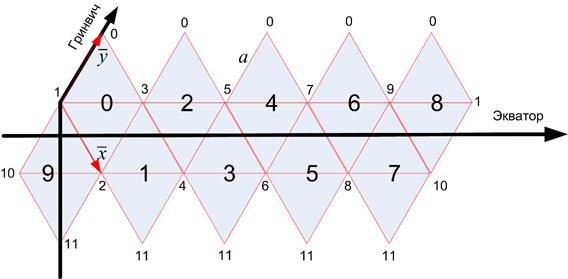
Рисунок 1 – Развертка икосаэдра применительно к географической системе координат
Расчет вершин икосаэдра (опорных точек) ${V}_{i}$ (где $i=0...11$) производится по формулам:
Широты опорных точек:
$$ \begin{matrix}
{\varphi}_{0}=\pi /2 \\
{\varphi}_{11}=- \pi /2 \\
{\varphi}_{1,3,5,7,9}=\pi /2 - \alpha \\
{\varphi}_{2,4,6,8,10}=- \pi /2 + \alpha
\end{matrix} \text{, (1)}$$
где $\alpha$ - угол между любыми соседними вершинами и вычисляется по формуле:
$$\alpha = 2 \cdot \arcsin \left( \frac{a}{2} \right) \text{, (2)}$$
здесь $a$ - длина ребра икосаэдра:
$$a = \frac{4}{\sqrt{2 \cdot \left( 5+\sqrt{5} \right)}} \text{, (3)}$$
Долготы опорных точек:
$$ \begin{matrix}
{\lambda}_{0,11}=0 \\
{\lambda}_{i=1...10}=\frac{2 \cdot \pi}{10} (i-1)
\end{matrix} \text{. (4)}$$
Переход от сферической системы координат к сегментной осуществляется в два этапа. На первом, определяется номер базового сегмента, в котором находится искомая точка $P$. Для этого необходимо определить, между какими опорными точками по долготе находится заданная точка:
$$ {\lambda}_{k+1} \leq \lambda (P) < {\lambda}_{(k+1) \mod 10 +1} \text{, (5)}$$
где $k$ вычисляется по формуле:
$$k=\left[ \frac{5 \cdot (( 2 \cdot \pi + \lambda (P)) \mod (2 \cdot \pi))}{\pi} \right] \text{, (6)}$$
затем, с помощью подстановки декартовых координат $P$ в уравнение плоскости ${V}_{(k+1)\mod 10+1}{V}_{k+1}O$ (где $O$ - начало координат), в зависимости от знака результата, определяется, к какому из двух возможных, верхнему (четному) или нижнему (нечетному) сегменту принадлежит заданная точка.
На втором этапе вычисляются значения локальных координат $\bar{x}$ и $\bar{y}$ в выбранном сегменте. Все базовые сегменты состоят из пары сферических треугольников $ABC$ и $ACD$ (рис.2), что бы минимизировать искажения, для каждого треугольника используется своя координатная полу-сеть, где средняя ось $\bar{xy}$ служит как недостающая ось для обоих полусегментов. Таким образом, две координатных полу-сети логически объединены в одну с осями $\bar{x}$ и $\bar{y}$.
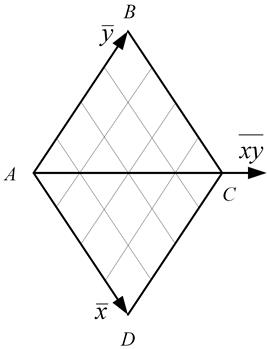
Рисунок 2 – Локальная система координат в базовом сегменте
Далее, проверяется положение точки $P$ относительно плоскости $ACO$, тем самым определяется полусегмент, которому принадлежит точка. Допустим, $P$ принадлежит $ABC$ (рис.3), для нахождения локальных координат нужно задать направляющие вектора ${N}_{x}$ и ${N}_{y}$, которые, по сути, являются осями пучков плоскостей, формирующих локальную координатную сетку. Они вычисляются следующим образом:
$${N}_{\bar{x}} = (A \times B) \times C \text{, (7)}$$
$${N}_{\bar{y}} = (B \times C) \times A \text{, (8)}$$
затем, определяются вектор $X$ как результат пересечения трех плоскостей:
$$X = {N}_{\bar{x}}OP \cap ACO \cap ABC \text{, (9)}$$
и $Y$ вектор :
$$Y = {N}_{\bar{y}}OP \cap ACO \cap ABC \text{. (10)}$$
Значения нормированных локальных координат будут:
$$\bar{x} = \frac{\angle XOA}{\alpha} \text{, (11)}$$
$$\bar{y} = \frac{\angle YOA}{\alpha} \text{. (12)}$$
Аналогично во втором полусегменте:
$${N}_{\bar{x}} = (C \times D) \times A \text{, (13)}$$
$${N}_{\bar{y}} = (A \times D) \times C \text{, (14)}$$
$$X = {N}_{\bar{x}}OP \cap ACO \cap ACD \text{, (15)}$$
$$Y = {N}_{\bar{y}}OP \cap ACO \cap ACD \text{, (16)}$$
$$\bar{x} = \frac{\angle XOA}{\alpha} \text{, (17)}$$
$$\bar{y} = \frac{\angle YOA}{\alpha} \text{. (18)}$$
В результате получаем координаты точки в виде $P=(j,\bar{x},\bar{y})$, где $j$ - номер сегмента.
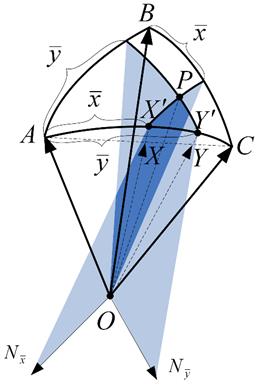
Рисунок 3 – Преобразование координат в базовом полусегменте
При обратном преобразовании координат из сегментных в сферические, полусегмент, которому принадлежит точка, определяется через сравнение $\bar{x}$ и $\bar{y}$. Если $\bar{x}$ меньше $\bar{y}$, значит, точка $P$ принадлежит сферическому треугольнику $ABC$, в противном случае принадлежит $ACD$. Затем, вычисляются точки $X'$ и $Y'$ на дуге $AC$. Это можно сделать различными способами, но наиболее наглядным будет поворот вектора $A$ на угол $\theta=\alpha \cdot t$ вокруг оси вращения $R=(x,y,z)=A \times C$, где $t$ принимает значение $\bar{x}$ для $X'$ и $\bar{y}$ для $Y'$. Матрица поворота $M(R,\theta)$ имеет вид:
$$M(R,\theta) = \left[ \begin{matrix}
\cos \theta + (1-\cos \theta)x^2 & (1-\cos \theta)xy-z \sin \theta & (1-\cos \theta)xz-y \sin \theta \\
(1-\cos \theta)xy-z \sin \theta & \cos \theta + (1-\cos \theta)y^2 & (1-\cos \theta)yz-x \sin \theta \\
(1-\cos \theta)xz-y \sin \theta & (1-\cos \theta)yz-x \sin \theta & \cos \theta + (1-\cos \theta)z^2
\end{matrix} \right] \text{. (19)}$$
Таким образом,
$$ X' = M(A \times C, \alpha \cdot \bar{x})\cdot A \text{, (20)}\\
y' = M(A \times C, \alpha \cdot \bar{y})\cdot A \text{, (21)}$$
Далее вычисляется точка $P$, как точка пересечения трех плоскостей, если искомая точка принадлежит треугольнику $ABC$:
$${N}_{\bar{x}} = (A \times B) \times C \text{, (22)}$$
$${N}_{\bar{y}} = (B \times C) \times A \text{, (23)}$$
$$P = {N}_{\bar{y}}OY' \cap {N}_{\bar{x}}OX' \cap ABC \text{, (24)}$$
если $ACD$:
$${N}_{\bar{x}} = (C \times D) \times A \text{, (25)}$$
$${N}_{\bar{y}} = (A \times D) \times C \text{, (26)}$$
$$P = {N}_{\bar{y}}OY' \cap {N}_{\bar{x}}OX' \cap ACD \text{, (27)}$$
затем, полученное значение $P$ нормируется или преобразуется в сферические (эллипсоидные) координаты.
Сегменты формируются путем деления базовых сегментов (уровень 1) на четыре дочерних сегмента второго уровня, каждый из которых может быть разбит на четыре сегмента третьего уровня и т.д. При этом любой сегмент любого уровня может быть рассчитан сразу, независимо от родителей. Чтобы оценить качество сегментации $\tau$ для разных уровней, была произведена оценка по трем параметрам (рис.4):
1) по длине хорды сегмента:
$$\tau = \frac{{L}_{max}}{{L}_{min}} \text{, (28)}$$
где ${L}_{max}$ наибольшая из хорд, а ${L}_{min}$ наименьшая.
2) по площади сегмента:
$$\tau = \frac{{S}_{max}}{{S}_{min}} \text{, (29)}$$
где ${S}_{max}$ наибольшая из площадей, а ${S}_{min}$ наименьшая.
3) по периметру сегмента:
$$\tau = \frac{{P}_{max}}{{P}_{min}} \text{, (30)}$$
где ${P}_{max}$ наибольший из периметров, а ${P}_{min}$ наименьший.
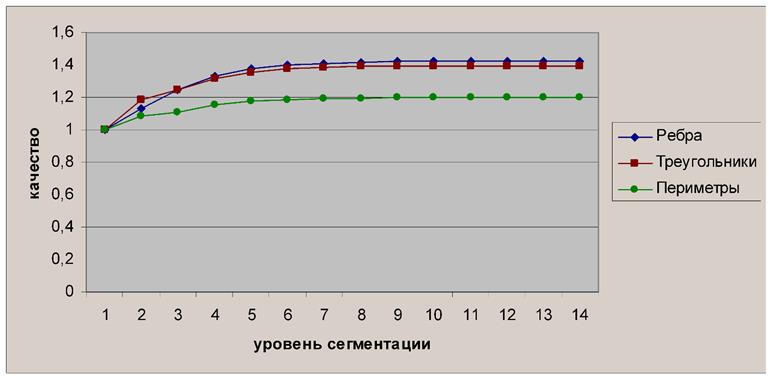
Рисунок 4 – Качество сегментации
Уровень 1 соответствует базовому сегменту, а качество равное 1 является эталонным. При сегментации сферы по геодезическим линиям ${L}_{max}$ будет бесконечно большим, а ${S}_{max}$ и ${P}_{max}$ будут стремиться к бесконечности.
В качестве упорядочивающей структуры дочерних сегментов, для каждого базового сегмента удобно использовать квадро-дерево [3]. Данный подход позволяет:
1) Производить эффективную отрисовку с быстрым отсечением невидимых сегментов. Во время обхода дерева достаточно проверить текущий узел дерева (сегмент) на пересечение с областью обзора, если они не пересекаются, то будет отброшена целая ветвь. Если же сегмент полностью попадает в область обзора, то можно отрисовывать все дочерние сегменты без дальнейших проверок.
2) Формировать сцену с динамической детализаций, поскольку каждому уровню дерева соответствует свой уровень детализации.
3) Осуществлять быстрый доступ к геоданным, при условии, что они будут связаны с сегментами.
Для быстрой отрисовки блоков ландшафта средствами видеопроцессора, необходимо определить минимальный уровень сегментации ${d}_{min}$, после которого допустимо применять линейную интерполяцию узлов сетки в декартовых координатах, вместо пересчета локальных координат сегмента в сферические (эллипсоидные), а затем только в декартовы. При этом, ${d}_{min}$ должен быть таким, чтобы изгиб горизонта выглядел плавно, а не грубой ломаной линией, и приближенно рассчитывается по формуле:
$${d}_{min} = \left] {\log}_{2} \frac{\alpha}{\arccos \left( 1-\frac{{k}_{1} \cdot \nu \cdot r}{{R}_{1} \cdot H} \right)} \right[ \text{, (31)}$$
где ${k}_{1}$ - максимальная ширина зазора между дугой и хордой на горизонте в пикселях, $r$ - расстояние до горизонта (радиус обзора), ${R}_{1}$ - среднее расстояние от начала координат $O$ до линии горизонта, $H$ - разрешение экрана по вертикали,
$$\nu = 2 \cdot \text{tg} ( \beta / 2) \text{, (32)}$$
где $\beta$ - вертикальный угол обзора камеры.
Максимальную относительную погрешность ${\Delta}_{max}$ при линейной интерполяции можно оценить по формуле:
$${\Delta}_{max} = \frac{{r}_{max}}{2 \cdot \sin (\alpha / 2^n)} \text{, (33)}$$
где $n$ - уровень сегментации (минимальное значение 1 соответствует базовому сегменту), ${r}_{max}$ максимальное из множества возможных значений $r=|P-P'|$ в сегменте уровня $n$, где $P$ - точная координата, а $P'$ - результат интерполяции. Для разных уровней сегментации ${\Delta}_{max}$ показано на графике (рис.5).
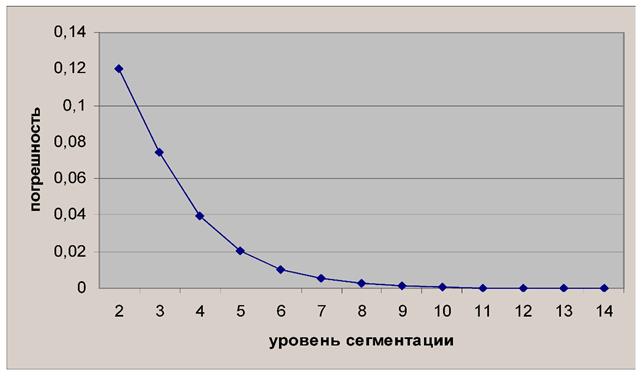
Рисунок 5 – Относительная погрешность линейной интерполяции
Помимо минимального уровня ${d}_{min}$ сегментации должен быть максимальный ${d}_{max}$, которым ограничивается точность карты, и достаточный уровень сегментации $d$, который можно рассчитать, как достаточную детализацию хорды на указанном расстоянии $l$ по формуле:
$$d = \left] {\log}_{2} \frac{\alpha \cdot {R}_{2} \cdot H}{{k}_{2} \cdot \nu \cdot l} \right[ \text{, (34)}$$
где ${R}_{2}$ - среднее расстояние от хорды до начала координат $O$, ${k}_{2}$ - минимально допустимая длина хорды в пикселях. Поскольку уровень детализации рассчитывается для хорд (сторон сегмента), детализация сегмента берется равной наибольшей из детализаций его сторон.
Для улучшения производительности пиксельных конвейеров видеопроцессора, необходимо в первую очередь отображать сегменты ближайшие к наблюдателю, чтобы отбросить как можно больше пикселей на этапе Z-буферизации. Этого легко достигнуть путем сортировки дочерних сегментов по условной дистанции в процессе обхода квадро-дерева. Условную дистанцию можно рассчитать как сумму расстояний до вершин сегмента. Аналогичным образом можно поступить с базовыми сегментами, что бы определить порядок обработки связанных с ними крвадро-деревьев.
На рисунках 6 и 7 изображен пример визуализации каркаса сферы размером с Землю, при моделировании были использованы числа с плавающей запятой двойной точности. Выделенные линии на рисунке 6 обозначают границы базовых сегментов.
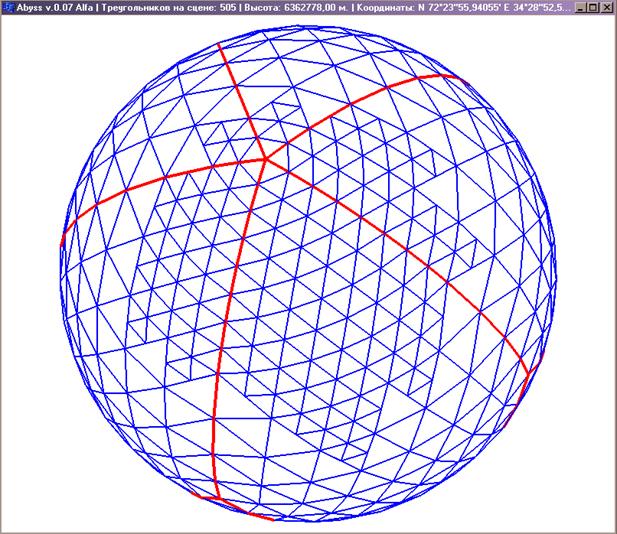
Рисунок 6 – Обзор с орбиты
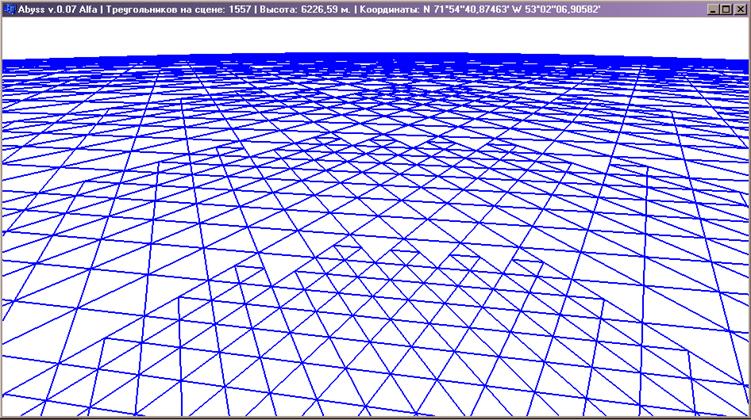
Рисунок 7 – Обзор у поверхности
При проектировании трехмерных ГИС, учебных и коммерческих приложений, предложенный метод позволяет реализовать прямую сегментацию поверхности с малыми искажениями, тем самым, обеспечивая качественную визуализацию и возможность реализации ландшафта планеты по векторному описанию с помощью тайлов, а совместно с технологией квадро-деревьев обеспечивает эффективные отрисовку и доступ к данным с географической привязкой. И поскольку преобразования координат связанные с методом сегментации обратимы, нет никакой сложности во взаимной конвертации геоданных между существующими ГИС и теми, что будут использовать предложенный метод.
Библиографический список
- Серапинас Б.Б., Математическая картография: Учебник для вузов / Балис Балио Серапинас. – М.: Издательский центр «Академия», 2005. – 336 с. ISBN 5-7695-2131-7.
- Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени: Пер. с нем./ Под ред. А.Н. Тюрина. – М.: Наука. Гл. ред. физ.-мат. лит., 1989. – 336 с. – ISBN 5-02-014197-6.
- ВМК МГУ, Спецкурс "ДОП. ГЛАВЫ МАШИННОЙ ГРАФИКИ", Использование квадро-деревьев, 2001 год. http://cylib.iit.nau.edu.ua/Mirrors/graphics.cs.msu.su/courses/index.html, дата получения документа 08.10.2007
 Проект эмуляции
Проект эмуляции