Технология аффинно-разностного кодирования для сжатия выборок цифровых сигналов
Аффинное или фрактальное [1] сжатие информации реализуется посредством самоподобия рассматриваемых данных, а декомпрессия выполняется путем итерации аффинных преобразований до достижения неподвижной точки.
Классические алгоритмы фрактального сжатия часто используют преобразование над дискретными значениями следующего вида:
$${x}_{i}={\bar{x}}_{i} \cdot k + \Delta \text{, (1)}$$
где ${x}_{i}$ – элемент сжимаемой последовательности данных, ${\bar{x}}_{i}$ – элемент преобразуемой к рассматриваемой последовательности, $k$ – коэффициент масштабирования, $\Delta$ – амплитудная поправка, а $i$ – номер элемента. Данный вид преобразования достаточно компактен, но малоэффективен на больших последовательностях данных, поскольку вероятность нахождения подходящего подобия с ростом длины резко падает, поэтому предлагается использовать модифицированную формулу:
$${x}_{i}= \left( i-\frac{n-1}{2} \right) \cdot h+{\bar{x}}_{i} \cdot k + \Delta \text{, (2)}$$
где, $n$ – размер последовательности, а $h$ – коэффициент искривления. Фактически, первый компонент суммы в формуле 2 является разностью прямых, которые наилучшим образом аппроксимируют рассматриваемую последовательность и подобие.
Для достижения неподвижной точки необходимо соблюсти два условия. Во-первых, длина исходной последовательности должна быть строго меньше длины подобия. Во-вторых, $k$ должен быть меньше единицы. В противном случае, если сжатые последовательности будут пересекаться с подобиями, возникнут искажения в восстанавливаемых данных, а неподвижная точка не будет достигнута.
Вычисление коэффициентов и поправки аффинного преобразования реализуется методом наименьших квадратов, который дает следующие системы линейных уравнений для формулы 1:
$$\left\{ \begin{matrix} k \cdot \sum {\bar{x}}_{i}^2 +\Delta \cdot \sum {\bar{x}}_{i} = \sum ( {\bar{x}}_{i} \cdot {x}_{i} ) \\ k \cdot \sum {\bar{x}}_{i} +\Delta \cdot n = \sum {x}_{i} \end{matrix} \right. \text{, (3)}$$
и для формулы 2:
$$ \left\{ \begin{matrix} k \cdot \sum {\bar{x}}_{i}^2 +\Delta \cdot \sum {\bar{x}}_{i} +h \cdot \sum \left( {\bar{x}}_{i} \cdot \left( i-\frac{n-1}{2} \right) \right) = \sum \left( {\bar{x}}_{i} \cdot {x}_{i} \right) \\ k \cdot \sum {\bar{x}}_{i} +\Delta \cdot n = \sum {x}_{i} \\ k \cdot \sum \left( {\bar{x}}_{i} \cdot \left( i-\frac{n-1}{2} \right) \right) + h \cdot \sum {\left( i-\frac{n-1}{2} \right) }^2 =\sum \left( {x}_{i} \cdot \left( i-\frac{n-1}{2} \right) \right) \end{matrix} \right. \text{. (4)}$$
Для подавляющего большинства небольших (до 6 элементов) последовательностей классическое аффинное преобразование дает пригодный результат не реже предложенного, но при этом оно требует хранить на один коэффициент меньше. Для последовательностей большей длины модифицированное преобразование дает значительно больше совпадений. Поэтому имеет смысл совместное применение обоих преобразований с разграничением области их применения. Чтобы повысить число подходящих подобий помимо прямого сравнения выполняется сравнение с разворотом подобия по нумерации элементов, таким образом, системы линейных уравнений 3 и 4 потребуется составлять и решать дважды.
Оценка потерь информации при аффинном кодировании производится через сравнение оригинальной последовательности данных и полученной по формуле 1 или 2 из рассматриваемого подобия.
Полный перебор при фрактальном сжатии дает наилучшие результаты, но требует огромных вычислительных ресурсов. В связи с этим предлагается ряд мер, направленных на существенное сокращение времени аффинного кодирования.
1. Поиск подобий достаточно производить только в уменьшенной в два раза копии выборки исходных данных. Отсюда ${\bar{x}}_{i}$ будет вычисляться по формуле:
$${\bar{x}}_{i} = \frac{{x}_{(s+i)\cdot 2}+{x}_{(s+i)\cdot 2+1}}{2} \text{, (5)}$$
где $s$ – смещение на последовательность подобия внутри уменьшенной копии выборки. При увеличении числа копий с различными масштабами разнообразие последовательностей растет незначительно, следовательно поиском подобий в других масштабах можно пренебречь. В ходе экспериментов по сжатию звуковых данных потери при переходе к фиксированному масштабу подобий составили менее десяти процентов, что отчасти компенсируется за счет меньшего объема кода для сжимаемой выборки, поскольку используется априорно известный коэффициент масштабирования подобий.
2. Длина последовательности $l$ берется в степени двух, но не меньше $2^2$, поскольку меньшую последовательность кодировать аффинным методом не выгодно, для этого будет применяться разностное кодирование. На практике потери от уменьшения вариаций длин последовательностей полностью компенсируются за счет перехода от линейного к логарифмическому росту величины $l$. Последовательности длиной $2^2$ кодируются под классическое аффинное преобразование, все остальные под модифицированное. При этом проверка на соответствие классическому преобразованию, также должна выполняться, поскольку коэффициент $h$ будет минимальным (равным нулю). Здесь, можно предложить три тактики поиска подобий в порядке возрастания вычислительных затрат: поиск до первого пригодного подобия, до первого пригодного классического подобия и полный перебор с выбором наилучшего подобия. Таким образом, аффинный код для последовательности будет состоять из значений $l$, $s$, $k$, $\Delta$, а также $h$ при $l>2$.
3. Ограничение числа экстремумов в сжимаемой последовательности и подобии позволяет увеличить скорость аффинного кодирования на несколько порядков без значительных потерь в степени сжатия. Чем больше экстремумов в последовательности, тем сильнее падает вероятность нахождения подобия. Рекомендуется ограничиться тремя экстремумами, что позволяет охватить более 90% подходящих аффинных преобразований. При поиске экстремумов в выборке необходимо учитывать допустимые потери информации, то есть экстремум фиксируется только в том случае, если он выходит за рамки допустимой с точки зрения потерь амплитуды.
4. Для ограничения числа не нужных проверок и вычислений по формулам 3 и 4, в качестве быстрого теста на соответствие введена проверка энергии сигнала и нормированных энергий гармоник ряда Фурье оригинальной последовательности и подобия с вычетом аппроксимирующей прямой. Энергия сигнала вычисляется по формуле:
$$E=\frac{2}{n} \cdot \sum {L}_{i}^{2} \text{, (6)}$$
где ${L}_{i}$ определяется формулой:
$${L}_{i} = {x}_{i} - \left( i - \frac{n-1}{2} \right) \cdot a-b \text{, (7)}$$
параметры $a$ и $b$ определяются методом наименьших квадратов:
$$ a = \frac{ \sum{ \left( \left( i - \frac{n-1}{2} \right) \cdot {x}_{i} \right) } }{ \sum {\left( i - \frac{n-1}{2} \right)}^2 } \text{, (8)} $$
$$b = \frac{\sum {x}_{i}}{n} \text{. (9)}$$
Нормированная энергия заданной гармоники определяется формулой:
$${E}_{j} = \frac{4}{{n}^2 \cdot E} \cdot \left( {\left( \sum \left( {L}_{i} \cdot \cos \frac{2 \cdot i \cdot j \cdot \pi }{n} \right) \right)}^2 + {\left( \sum \left( {L}_{i} \cdot \sin \frac{2 \cdot i \cdot j \cdot \pi }{n} \right) \right)}^2 \right) \text{, (10)}$$
здесь $j$ – номер гармоники. Энергии для выборки подобий рассчитываются аналогично и заранее для всех допустимых по количеству экстремумов подобий. Порог расхождения энергий оригинальной последовательности и подобия рассчитывается исходя из допустимых потерь:
$$p = \sqrt{ \frac{2 \cdot \sum {f}^2 ({L}_{i})}{n \cdot E} }-1 \text{, (11)}$$
где $f({L}_{i})$ дополненный погрешностью сигнал с вычетом аппроксимирующей прямой, например, при заданном максимальном отклонении $d$ от оригинальной последовательности $f({L}_{i})$ примет вид:
$$f({L}_{i}) = \left\{ \begin{matrix} {L}_{i}+d, & для & {L}_{i}>0 \\ {L}_{i}-d, & для & {L}_{i}<0 \\ 0, & для & {L}_{i}=0 \end{matrix} \right. \text{. (12)}$$
Условием для дальнейшей проверки подобия на совпадение с оригинальной последовательностью будет:
$$\left\{ \begin{matrix} \sqrt{ \bar{E}} \geq \sqrt{E} \cdot (1-p) \\ \left| \sqrt{ {\bar{E}}_{j}} - \sqrt{ {E}_{j}} \right| \geq p \end{matrix} \right. \text{, (13)}$$
где $\bar{E}$ и ${\bar{E}}_{j}$ – энергии, рассчитанные для подобия. Опытным путем было установлено, что достаточно использования энергии первых трех-четырех гармоник, это позволяет сократить время поиска подобий на порядок.
5. Ограничение области поиска подобий. Для этого уменьшенная выборка рассматривается как кольцо, а область поиска ограничивается скользящим окном, центр которого располагается в точке соответствующей началу рассматриваемой последовательности в выборке подобий. Данный прием позволяет настраивать процесс аффинного кодирования между степенью и скоростью сжатия.
Полученные аффинные параметры $l$, $s$, $k$, $\Delta$ и $h$ необходимо привести к виду удобному для сжатия различными энтропийными методами [2], которые позволяют получить дополнительный выигрыш в процессе архивации. Параметр длины последовательности $l$ преобразуется следующим образом:
$l=0$ – резервируется для обозначения начала блока разностного кода, в котором сначала указывается количество разностей $c$, а затем размещается дельта-код в указанном объеме.
$l = \pm (l-1)$ – кодирует длину кода в виде ${2}^{|l|+1}$, а знак указывает на то, в каком виде используется подобие: развернутом или нормальном порядке следования элементов. Далее, коэффициент искривления $h$ преобразуется к целому числу с фиксированной точкой, число разрядов за которой равно $|l|+1$. Коэффициент масштабирования $k$ также преобразуется к целому с фиксированной точкой, но число разрядов ${r}_{k}$ рассчитывается, как двоичный логарифм от среднеквадратичной максимальной разности амплитуд в допустимых последовательностях подобий:
$${r}_{k} = {\log}_{2} \left( \sqrt{\frac{\sum {\left( \text{max}({\bar{x}_{s}}...{\bar{x}_{s+m-1}}) - \text{min}({\bar{x}_{s}}...{\bar{x}_{s+m-1}}) \right)}^2 }{M}} \right) \text{, (14)}$$
где $m={2}^{|l|+1}$ – длина рассматриваемого подобия, а $M$ - количество допустимых к использованию подобий. Амплитудная поправка $\Delta$ округляется до ближайшего целого значения. Затем $l$, $\Delta$ и $h$ преобразуются в беззнаковую форму посредством следующей функции:
$$z(\nu) = \left\{ \begin{matrix} -2 \cdot \nu, & для & \nu \leq 0 \\ 2 \cdot (\nu-1)+1, & для & \nu > 0 \end{matrix} \right. \text{, (15)}$$
где под значением $\nu$ понимается один из параметров $l$, $\Delta$ или $h$. Коэффициент масштабирования $k$ в большинстве случаев бывает ближе к своему максимуму ${k}_{\text{max}}$, чем к нулю, поэтому преобразование к беззнаковой форме имеет вид:
$$k' = \left\{ \begin{matrix} 2 \cdot ({k}_{\text{max}}+k)+1, & для & k<0 \\ 2 \cdot ({k}_{\text{max}}-k), & для & k \geq 0 \end{matrix} \right. \text{. (16)}$$
Смещение на последовательность подобия $s$ в процессе сжатия реализуется как инкрементная переменная, которая уже считается закодированной и помещается в архив без изменений, но при доступе к подобию она декодируется в два этапа:
$$ s' = \left\{ \begin{matrix} \frac{s}{2}+1+t, & для & s \mod 2 >0 \\ - \frac{s}{2}+t, & для & s \mod 2 = 0 \end{matrix} \right. \text{, (17)} $$
где $t$ – смещение на кодируемую или декодируемую последовательность, второй этап выполняет поправку смещения в кольце:
$$ s''=\left\{ \begin{matrix} s'-N, & для & s' \geq N \\ s'+N, & для & s' < 0 \\ s', & для & 0 \leq s' < N \end{matrix} \right. \text{. (18)} $$
Преобразованные параметры аффинных кодов и результаты дельта-кодирования представляют собой целые числа, которые могут быть в дальнейшем подвергнуты статистическому сжатию или преобразованы в префиксные коды [3].
Разностное кодирование предлагается использовать там, где аффинное кодирование недостаточно эффективно или не было найдено удовлетворяющих заданной точности подобий. Для этого был разработан алгоритм разностного кодирования с уровневой адаптацией. Нулевой уровень разности говорит о том, что данные записываются как есть, первый уровень соответствует классическому алгоритму, на втором уровне последовательность данных представляется в форме разности разностей и так далее до бесконечности. Критерием изменения уровня на следующем шаге служит факт того, что абсолютное значение разности текущего уровня больше абсолютного значения наименьшей из разностей других уровней. Обычно достаточно ограничиться вторым уровнем разности, который соответствует скорости изменения кодируемого значения. На рисунке 1 показан пример кодирования исходных данных (график с тонкой линией) в разностную форму (нижний график с толстой линией). В верхней части рисунка отмечены изменения уровня разности в процессе адаптации. Степень положительного эффекта от разностного кодирования во многом будет зависеть от характера данных, но даже если данные будут крайне зашумленными, благодаря адаптивности алгоритма, вероятность возникновения отрицательного эффекта будет минимальной.
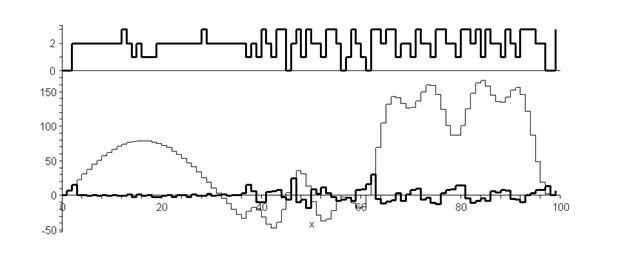
Рис. 1. Пример разностного кода с уровневой адаптацией
Для улучшения степени сжатия выборки дополнительно рекомендуется провести отсев неэффективных аффинных кодов. Для этого можно выполнить три прохода по полученным кодам. В первый проход дельта-кодом заменяются пары соседних аффинных кодов, если их суммарный условный объем больше объема дельта-кода для последовательностей которые они кодируют. Условный объем вычисляется как сумма логарифмов по основанию два от элементов кода. Второй и третий проходы расширяют области разностного кода вправо и влево, путем проверки прилегающих к дельта-кодированным областям аффинных кодов на необходимость их присоединения с точки зрения условного объема.
Для восстановления сигнала из архива необходимо в первом проходе по кодированным данным восстановить дельта кодированные последовательности. Затем, выполняется множество проходов, в которых выполняются аффинные преобразования по функциям 1 и 2, параметры которых записаны в аффинных кодах, до тех пор, пока не будет достигнута неподвижная точка. Признаком неподвижной точки служит факт того, что для всех элементов выборки разница между старым значением ${x}_{i}$ и новым ${x'}_{i}$ в рамках текущего прохода не превышает единицы. На рисунке 2 приведен пример отклонения восстановленного сигнала от оригинала в процентах, при кодировании максимально допустимое отклонение было ограниченно величиной 0.05% от максимальной амплитуды. Участки с нулевым отклонением соответствуют дельта-кодированным последовательностям.

Рис. 2. Пример отклонения восстановленного сигнала от оригинала
В ходе экспериментов было установлено, что среднеквадратичное отклонение от оригинала составляет $0.5 \cdot d$, а максимальное отклонение $2 \cdot d$. По степени сжатия на примере звуковых файлов, как самых популярных объектов сжатия, при сходных потерях данная технология превзошла все известные алгоритмы, даже без использования дополнительного статистического кодирования. Это обусловлено поточной ориентацией алгоритмов сжатия звука и сигналов в целом, архиваторов не ориентированных на поток выявлено не было.
Библиографический список
- Ватолин Д., Ратушняк А., Смирнов М., Юкин В. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео. – М.: ДИАЛОГ-МИФИ, 2003. – 384 с.
- Сэломон Д. Сжатие данных, изображений и звука. М.: Техносфера, 2004. 368 с.
- Fenwick P. Punctured Elias Codes for variable-length coding of the integers. // Department of Computer Science, The University of Auckland. – Technical Report 137. – 5 December 1996.
 Проект эмуляции
Проект эмуляции