Префиксный код с регулируемым приращением
- близкий к логарифмическому характер роста;
- регулируемый шаг роста размера кода.
Для выполнения поставленных требований было разработано семейство префиксных кодов формата $p \times q(s)$. Данный метод префиксного кодирования здесь и далее будет обозначаться как PQS-код. Данный формат предусматривает: префикс переменной длины, кодирующий номер интервала чисел, с шагом приращения $p$; индекс в заданном интервале с шагом приращения $q$; модификатор начального интервала $s$.
Модификация начального интервала служит для компактного представления малых значений, при параметре $s$ меньшем нуля, или удлинения начального интервала, при параметре $s$ большем нуля, но меньшем $q$, с целью компенсировать какие-либо всплески в статистике кодируемых значений, например при разностном кодировании цифровых сигналов часто возникающие в процессе адаптации к характеру поступающей информации. При $s$ меньше нуля, используется дополнительный интервал, кодируемый числом из $\left( -s \right)$ бит, диапазон значений соответствующий интервалу будет $\left[0; \bar{ L } \right)$, где $ \bar{ L } = 2^{ -s } -1 $. Все числа выходящие за рамки диапазона дополняются префиксом из $\left( -s \right)$ единиц.
Параметр удлинения начального интервала $h$ определяется выражением:
$$h = \left\{\begin{matrix} s &при &s>0 \\ 0 &при &s\leq 0 \end{matrix}\right. \text{.}$$
Длина начального интервала определяется формулой:
$${L}_{0} = \left( 2^h-1 \right) \cdot 2^{q-h} + 2^q,$$
отсюда диапазон значений $\left[0; {L}_{0} \right)$, которые линейно кодируются $p+q$ битами. Оставшиеся интервалы в рамках первого шага префикса имеют длину:
$${L}_{i} = 2^{q \cdot \left( i+1 \right)},$$
где номер интервала $i$ меняется от 1 до $2^p-2$. При этом код индекса $I'$ в данных интервалах не эквивалентен его линейному значению $I$ и вычисляется по формуле:
$$I' = \left( I + {L}_{i} - 2^{q \cdot \left( i+1 \right) -h} \right) \text{mod} {L}_{i}.$$
Длины дальнейших интервалов $i = 2^p -1 ... \infty$ определяются формулой:
$${L}_{i} = 2^{q \cdot \left( i+1 \right) -h} .$$
Индекс кодируется линейно, а старшая часть длиной $h$ бит заполняется единицами и присоединяется к первой части префикса.
При декодировании номер интервала определяется формулой:
$$ i= \frac{ \frac{ {Q}_{0} }{2^{q-h}} +1 }{2^h}+\sum{ {P}_{j} } , $$
где ${Q}_{0}$ – начальный элемент индекса, а ${P}_{j}$ элементы префикса кода длиной по $p$ бит. Если ${P}_{j}$, содержит значение $2^p-1$, это говорит о том, что впереди есть еще один элемент ${P}_{j+1}$, здесь $j$ может меняться от одного до бесконечности. Количество разрядов $N$ отведенных под значение индекса заданного интервала вычисляется по формуле:
$$N = \left\{\begin{matrix} q+h &при &i=0 \\ \left( i+1 \right) \cdot q &при & i \leq 2^p-2 \\ \left( i+1 \right) \cdot q -h &при & i \geq 2^p-1 \end{matrix}\right. \text{,}$$
Максимальное значение индекса для заданного интервала с учетом возможных модификаций начального интервала можно представить формулой:
$$ V\left(i\right) = \bar{L} -1+\sum{{L}_{i}},$$
при этом кодируемые в интервале числа будут ограничены значениями от $ V\left(i-1\right)+1$ до $ V\left(i\right)$ включительно, при этом принять $ V\left(-1\right) = -1$.
Примеры построения некоторых префиксных кодов из предложенного PQS-семейства и упомянутых кодов Голомба и Омега-кода Элиаса приводятся в таблице №1.
| Двоичное число | Омега-код Элиаса | Код Голомба m=5 | PQS код формата 1x1(-1) | PQS код формата 1x2(0) | PQS код формата 2x2(1) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 000 | 0000 |
| 1 | 100 | 1 | 100 | 010 | 0010 |
| 10 | 110 | 10 | 101 | 001 | 0001 |
| 11 | 101000 | 110 | 11000 | 011 | 0011 |
| 100 | 101100 | 111 | 11100 | 100000 | 1000 |
| 101 | 101010 | 1000 | 11001 | 110000 | 1010 |
| 110 | 101110 | 1001 | 11101 | 101000 | 100100 |
| 111 | 1110000 | 1010 | 1101000 | 111000 | 101100 |
| 1000 | 1111000 | 10110 | 1111000 | 100010 | 100110 |
| 1001 | 1110100 | 10111 | 1101100 | 110010 | 101110 |
| 1010 | 1111100 | 11000 | 1111100 | 101010 | 100101 |
| 1011 | 1110010 | 11001 | 1101001 | 111010 | 101101 |
| 1100 | 1111010 | 11010 | 1111001 | 100001 | 100111 |
| 1101 | 1110110 | 110110 | 1101101 | 110001 | 101111 |
| 1110 | 1111110 | 110111 | 1111101 | 101001 | 10000 |
| 1111 | 10100100000 | 111000 | 110101000 | 111001 | 11000 |
| 10000 | 10100110000 | 111001 | 111101000 | 100011 | 10010 |
| 10001 | 10100101000 | 111010 | 110111000 | 110011 | 11010 |
| 10010 | 10100111000 | 1110110 | 111111000 | 101011 | 10001 |
| 10011 | 10100100100 | 1110111 | 110101100 | 111011 | 11001 |
| 10100 | 10100110100 | 1111000 | 111101100 | 100100000 | 10011 |
| 10101 | 10100101100 | 1111001 | 110111100 | 110100000 | 11011 |
| 10110 | 10100111100 | 1111010 | 111111100 | 101100000 | 1010000 |
| 10111 | 10100100010 | 11110110 | 110101001 | 111100000 | 1110000 |
| 11000 | 10100110010 | 11110111 | 111101001 | 100110000 | 1011000 |
| 11001 | 10100101010 | 11111000 | 110111001 | 110110000 | 1111000 |
| 11010 | 10100111010 | 11111001 | 111111001 | 101110000 | 1010100 |
| 11011 | 10100100110 | 11111010 | 110101101 | 111110000 | 1110100 |
| 11100 | 10100110110 | 111110110 | 111101101 | 100101000 | 1011100 |
| 11101 | 10100101110 | 111110111 | 110111101 | 110101000 | 1111100 |
| 11110 | 10100111110 | 111111000 | 111111101 | 101101000 | 1010010 |
| 11111 | 101101000000 | 111111001 | 11010101000 | 111101000 | 1110010 |
Характер роста размеров префиксных кодов относительно размера кодируемого числа показан на рисунке 1, размеру числа соответствует нижний график. Жирной линией выделен график демонстрирующий рост PQS-кода формата 1x3(0), чуть выше его огибает график для Омега-кода Элиаса. График с линейным ростом соответствует коду Голомба с m=511.
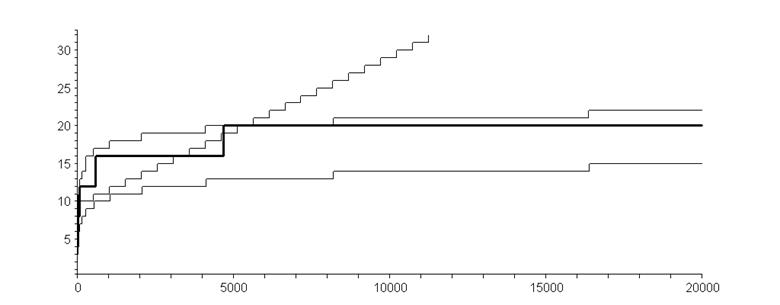
Рис. 1. Графики роста префиксных кодов
Различие PQS-кодов с нормальным и удлиненным начальным интервалами показывает заштрихованная область на рисунке 2. За выигрыш выделенного толстой линией PQS-кода формата 1x4(2) относительно пересекающегося с ним PQS-кода формата 1x4(0) в начальном диапазоне, на последующих диапазонах приходится платить существенным отставанием, таким образом, за счет параметра можно подстраиваться под статистику кодируемых данных.
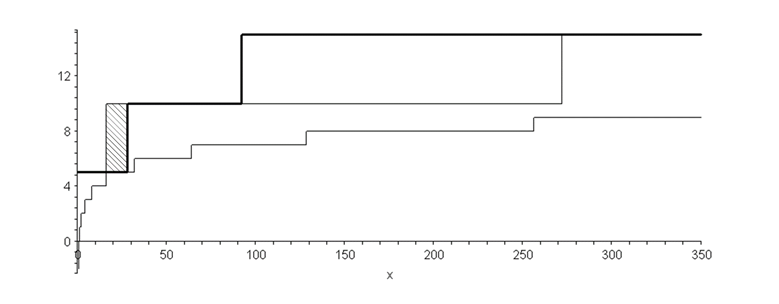
Рис. 2. Пример использования дополнительного интервала PQ-кода
Предложенный метод префиксного кодирования встраивается не только в бинарные, но и в текстовые форматы данных путем использования подмножества алфавита, размер которого должен быть равен степени двойки. Например, для обычной шестнадцатеричной строки можно воспользоваться PQS-кодом формата 1x3(0,1,2) или 4х4(0,1,2,3).
Библиографический список
- Fenwick P. Punctured Elias Codes for variable-length coding of the integers. // Department of Computer Science, The University of Auckland. – Technical Report 137. – 5 December 1996.
 Проект эмуляции
Проект эмуляции