Комбинаторное кодирование информации
Суть комбинаторного метода заключается в том, что из известных алфавита и таблицы частот, можно сформировать строго определенное число различных последовательностей данных. Таким образом, каждой последовательности данных, ставится в соответствие строго определенный (комбинаторный) номер (код) и, наоборот, каждому комбинаторному номеру строго определенная последовательность данных. Развивая эту идею можно предложить использование развернутых статистик, включающих частоты повторов по каждому символу и частоты соседства символов друг с другом.
Исходную последовательность данных можно представить в виде массива $D\left[N\right]$, где $N$ – количество элементов сжимаемой выборки. При сканировании массива $D\left[N\right]$ формируется расширенная статистика, которая представлена четырьмя таблицами:
- $A\left[n\right]$ – символы алфавита, упорядоченные по возрастанию;
- $F\left[n\right]$ – частоты встреч символов алфавита в рассматриваемых данных;
- $M\left[n\right]$ – частоты повторов символов алфавита;
- $K\left[n\right]\left[n\right]$ – частоты корней и префиксов;
где, $n$ – размер алфавита. В последнем массиве под понятием корня подразумевается пара символов исходной последовательности $D\left[i\right]$ и $D\left[i+1\right]$, такая что $D\left[i\right]<D\left[i+1\right]$, в противном случае $D\left[i\right]$ воспринимается в качестве префикса, а ячейка $K \left[ T\left( D\left[i\right] \right) \right] \left[ T\left( D\left[i+1\right] \right) \right] $ содержит число подобных событий, где функция $T\left(x\right)$ вычисляет порядковый номер рассматриваемого символа в алфавите. Таким образом, верхняя правая половина матрицы содержит статистику корней, а нижняя левая, включая диагональ, содержит статистику префиксов. На рисунке 1 приведен пример разбиения последовательности на слова, при этом содержимое таблиц статистики будет иметь вид:
$$A\left[4\right]=\left\{\begin{matrix}a&b&c&d\end{matrix}\right\},$$
$$F\left[4\right]=\left\{\begin{matrix}2&3&4&3\end{matrix}\right\},$$
$$M\left[4\right]=\left\{\begin{matrix}0&1&2&2\end{matrix}\right\},$$
$$K\left[4\right]\left[4\right]=\left\{\begin{matrix}0&2&0&0\\0&0&1&0\\1&0&1&1\\0&0&1&1\end{matrix}\right\}.$$

Рис. 1. Пример разбиения последовательности на слова
Кодирование последовательности по полученной статистике может быть выполнено одним из трех способов, в зависимости от того какой из них эффективнее в конкретной ситуации:
- простое комбинаторное кодирование на основе таблицы частот $F\left[n\right]$;
- серийное комбинаторное кодирование с учетом повторов символов на основе таблицы повторов $M\left[n\right]$ и ее разности с таблицей частот $F\left[n\right]-M\left[n\right]$;
- словарное комбинаторное кодирование с учетом соседства символов на основе таблицы корней и префиксов $K\left[n\right]\left[n\right]$ .
Все перечисленные способы комбинаторного кодирования строятся на основе числа возможных сочетаний или биномиальных коэффициентов [1, 2]. Номер сочетания определяется согласно алгоритму изображенному на рисунке 2. Есть некоторая булева последовательность $L\left[t+f\right]$, состоящая из $t$ истинных и $f$ ложных значений. При сканировании данной последовательности ее инициализированный нулем номер сочетания $I$ в случае истинного значения будет увеличиваться на количество комбинаций, которые могли бы быть составлены из остатка последовательности, если бы текущий элемент был заменен ложным из оставшихся элементов.
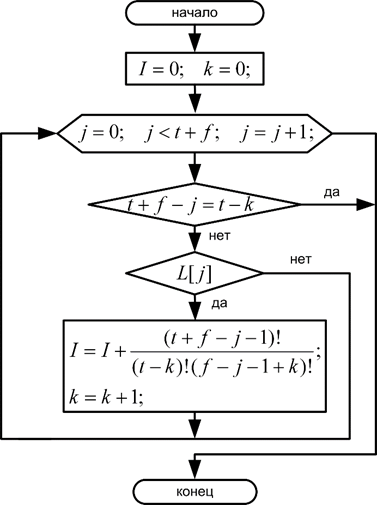
Рис. 2. Алгоритм вычисления номера сочетания
Процесс восстановления булевой последовательности по номеру сочетания $I$ и указанной статистики истинных $t$ и ложных $f$ значений представлен на рисунке 3. Здесь необходимо отметить, что факториал нуля равен единице.
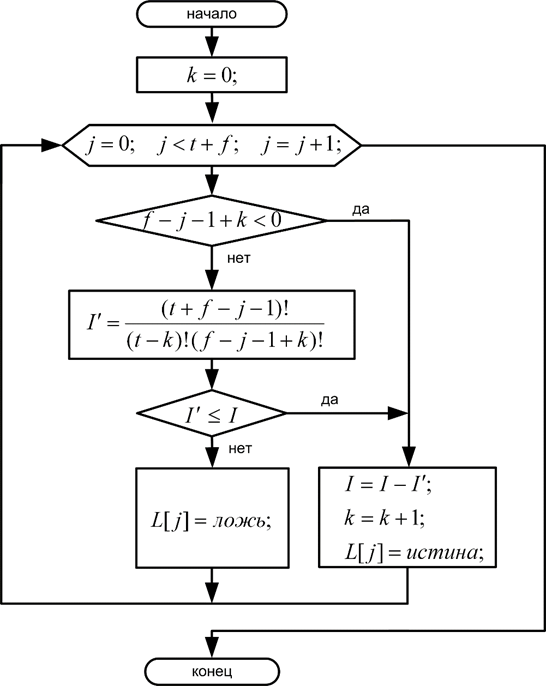
Рис. 3. Алгоритм восстановления булевой последовательности
Простое комбинаторное кодирование заключается в вычислении кода ограниченного мультиномиальным коэффициентом:
$${V}_{N} = {C}_{M}\left( F\left[ 0...n-1\right] \right) = \frac{ \left( \sum_{i=0}^{n-1}{F\left[i\right]} \right)! }{ \prod_{i=0}^{n-1}{ F\left[i\right]! } } \text{. (1)}$$
Процесс простого комбинаторного кодирования при этом можно записать в виде выражения:
$${R}_{N} = \bar{C}\left( D\left[0...N-1\right]\right) = \sum_{i=0}^{n-2}{ \left[ {E}_{N}\left( F[i], \sum_{j=i+1}^{n-1}{F[j]},{D}_{i},A[i] \right) \cdot {C}_{M}(F[i+1...n-1]) \right] }, $$
Серийный комбинаторный код тесно связан с другим алгоритмом сжатия – кодированием длин серий. Интересный факт: каждый элемент, кодирующий длину серии, является частным случаем простого комбинаторного кода нулевого размера. Оригинальная последовательность $D[N]$ предварительно должна быть преобразована в разделенный на два массива код длин серий, где $D'[N']$ содержит символы, а $A[N']$ длины серий. Ограничение серийного комбинаторного кода определяется формулой:
$${V}_{S} = {C}_{M}(FM[0...n-1])\cdot \hat{C} (F[0...n-1],M[0...n-1]) \text{, (2)}$$
где $\hat{C}$ вычисляется по формуле:
$$\hat{C} (F[0...n-1],M[0...n-1]) = \prod_{i=0}^{n-1}{ C(F[i]-1,M[i]) },$$
здесь и далее $C$ – биномиальный коэффициент. Таблица $FM[n]$ является разностью таблиц частот и повторов $F[n]-M[n]$. Процесс серийного комбинаторного кодирования определяется выражением:
$${R}_{S} = \bar{C}(D'[0...N'-1])+{C}_{M}(FM[0...N-1]) \cdot \sum_{i=0}^{n-1}{\left[ {E}_{S}(M[i],F[i]-1-M[i],D',S,A[i]) \cdot \hat{C}(F[0...i-1],M[0...i-1]) \right]}. $$
Функция ${E}_{S}(...)$ вычисляет номер сочетания $I$ для булевой последовательности с $M[i]$ истинных значений и $F[i]-M[i]-1$ ложных значений из элементов кода длин серий, чей код символа равен $A[i]$. Булева последовательность формируется при сканировании кодов длин серий, если $D'[j]$ эквивалентен $A[i]$, то записывается $S[j]$ истинных значений и одно ложное, кроме самого последнего. Процесс декодирования строится обратно процессу кодирования, при этом требуются алфавит, таблица повторов и разность таблицы частот и повторов.
Словарное комбинаторное кодирование использует разбиение исходной последовательности данных на части (слова) $W[N'']$ состоящие из корня и префиксов (рис. 1). Исключением является последнее слово, которое может быть пустым, как в проиллюстрированном примере, или состоять из одних лишь префиксов. Каждое слово рассматривается как стек с вершиной при последнем символе. При этом код будет ограничен значением:
$${V}_{W} = U \cdot Q \cdot \prod_{i=0}^{n-1}{ C(G(i)+K[i][i],G(i))}\text{, (3)}$$
$$ U = \frac{\left( \sum_{i=0}^{n-2}{\sum_{j=i+1}^{n-1}{K[i][j]}} \right)!}{ \prod_{i=0}^{n-2}{\prod_{j=i+1}^{n-1}{K[i][j]}}! }, $$
$$ Q = \prod_{i=0}^{n-1}{\prod_{j=0}^{i-1}{ C(H(i,j),K[i][j]) }}, $$
$$ G(i) = \sum_{j=i+1}^{n-1}{K[i][j]}+{q}_{i}-1, $$
$$ H(i,j) = \sum_{k=j+1}^{n-1}{K[j][k]} - \sum_{k=j+1}^{i-1}{K[k][j]}+{q}_{j}, $$
где ${q}_{i}$ и ${q}_{j}$ определяются выражением:
$$ {q}_{i} = \left\{ \begin{matrix} 1&при&D[N-1]=A[i] \\0&при&D[N-1]\neq A[i] \end{matrix}\right. .$$
Процесс вычисления словарного комбинаторного кода можно записать в виде следующих выражений:
$${R}_{W} = \sum_{i=0}^{n-1}{\left[ \sum_{j=i+1}^{n-1}{ \left[ {E'}_{N}(K[i][j],P(i,j),W,A[i],A[j]) \cdot U'(i,j) \right] } \\+ U \cdot \sum_{j=0}^{i-1}{ \left[ {E''}_{N} (K[i][j],H(i,j),W,A[i],A[j]) \cdot Q'(i,j) \right] } \\+ U \cdot Q \cdot {E'}_{S}(K[i][i],G(i),W,A[i]) \cdot \prod_{j=0}^{i-1}{C(G(j)+K[j][j],G(j))} \right]}, $$
$$P(i,j) = \sum_{k=j+1}^{n-1}{K[i][k]}+ \sum_{t=i+1}^{n-2}{ \sum_{k=t+1}^{n-1}{K[t][k]} }, $$
$$ U'(i,j) = \frac{ \left( \sum_{t=i+1}^{n-2}{ \sum_{k=t+1}^{n-1}{ K[t][k] } } + \sum_{k=j+1}^{n-1}{K[i][k]} \right) ! }{ \prod_{t=i+1}^{n-2}{ \prod_{k=t+1}^{n-1}{ K[t][k]! } } \cdot \prod_{k=j+1}^{n-1}{K[i][k]!} }, $$
$$ Q'(i,j) = \prod_{t=1}^{i-1}{ \prod_{k=0}^{t-1}{ C(H(t,k),K[t][k]) } } \cdot \prod_{k=0}^{j-1}{C(H(i,k),K[i][k])}. $$
Формирование словарного кода выполняется по строкам таблицы корней и префиксов, каждая строка обрабатывается в три этапа. На первом этапе кодируются корни функцией ${E'}_{N}(...)$, аналогично простому комбинаторному коду для символов, при этом, если в стеке слова найден искомый корень, последний элемент удаляется из стека. Совпадающие с искомым корни кодируются как истинные значения, а несовпадающие, как ложные. Второй этап кодирует все префиксы до диагонального элемента. Функция ${E''}_{N}(...)$ аналогична предыдущей процедуре, но рассматриваются префиксы, а не корни. Заключительный этап кодирует повторяющиеся символы функцией ${E'}_{S}(...)$ подобно серийному коду с тем исключением, что подсчет длин серий происходит по мере сканирования слов. По окончанию кодирования все стеки становятся пустыми (содержат лишь первый символ слова), а в процессе декодирования они наполняются и затем складываются в исходную последовательность данных. Для успешного декодирования необходимо знать алфавит, таблицу корней и префиксов, а также порядковый номер последнего символа последовательности данных в алфавите, если последнее слово не является пустым.
Минимальное число бит необходимое для хранения комбинаторного кода определяется выражением $B=\left] {\log}_{2}(V-1) \right[$, при значении $V$ равном единице, размер кода берется равным нулю. В программной реализации, вычисление логарифма заменяется сканированием числа $V$ до первой значащей двоичной единицы, подобно ассемблерной команде BSR [3].
В отличие от арифметического сжатия и метода Хаффмана [4], для которых событием является очередной символ последовательности данных с информационной энтропией ${H}_{0} = - \sum_{i=0}^{n-1}{\left( \frac{F[i]}{N} \cdot {\log}_{2} \left( \frac{F[i]}{N} \right) \right)}$, для комбинаторного сжатия событием является вся последовательность данных со всеми зависимостями, отраженными статистикой. Это позволяет повысить эффективность сжатия относительно энтропии нулевого порядка при сохранении универсальности в отношении потока данных. Например, для простого комбинаторного кодирования суммарная условная энтропия $N$ порядка ${H}_{SN}={\log}_{2}({V}_{N})$, а затраты на хранение комбинаторного кода можно записать, как $B=\left] {H}_{SN} \right[$.
Для повышения эффективности комбинаторного кодирования необходимы механизмы разбиения потока данных на блоки с учетом трех вариантов кода, поскольку алгоритм не является адаптивным.
Для разбиения данных на блоки предлагается способ, который состоит из двух этапов. Первый этап выполняется в процессе сбора статистики данных, в ходе которого проверяются два условия, выполнение любого из которых приводит к формированию нового блока:
- если расчетный результат простого комбинаторного кодирования меньше размера оригинальной последовательности в Омега-кодах Элиаса, но среднее число бит в расчете на один элемент последовательности увеличилось;
- если отдельно взятый размер простого комбинаторного кода больше собственной статистики в Омега-кодах Элиаса и среднее число бит на элемент увеличилось.
Простое комбинаторное кодирование в процессе разбиения выполнять не требуется, достаточно приближенно рассчитать размер кода по мере формирования статистики. Изменение числа возможных сочетаний ${V}_{N}$ по мере поступления данных ${d}_{i}$ можно представить формулой:
$${V}_{N}(i) = {V}_{N}(i-1) \cdot \frac{i}{f({d}_{i})+1}, $$
где $f({d}_{i})$ – число символов эквивалентных ${d}_{i}$ в уже рассмотренных данных, при этом ${V}_{N}(0)=1$. Отсюда приближенный размер простого комбинаторного кода ${B'}_{N}$ будет меняться согласно выражению:
$${B'}_{N}(i) = {B'}_{N}(i-1)+{\log}_{2}(i)-{\log}_{2}(f({d}_{i})+1).$$
Второй этап начинается с построения дерева объединений статистик $S$ полученных на первом этапе (рис.4). Построение дерева происходит снизу вверх, при этом будет создано не более $n-1$ новых статистик. Данное дерево является условно двоичным, поскольку одиночные статистики, которым не хватило пары, складываются с последней парой. Для корректного суммирования двух соседних статистик для всех вариантов комбинаторного кода на первом этапе потребуется соблюсти дополнительное условие: текущий блок должен заканчиваться словом, а последний символ блока не должен повторяться в начале следующего блока, либо необходимо учитывать подобное событие.
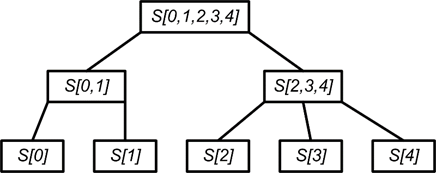
Рис. 4. Простой пример дерева статистик
В процессе построения дерева рассчитывается минимальный размер комбинаторного кода для каждого узла с учетом трех вариантов кодирования и варианта, когда кодирование не оправдано. Размеры серийного и словарного комбинаторного кода вычисляются приближенно с использованием формулы Муавра-Стирлинга [5], а также формул (2) и (3):
$$ {B'}_{S} = \phi \left( \sum_{i=0}^{n-1}{FM[i]} \right) - \sum_{i=0}^{n-1}{ \phi (FM[i])} + \sum_{i=0}^{n-1}{\left( \phi (F[i]-1)-\phi (M[i]) - \phi (F[i]-M[i]-1) \right) }, $$
$$ {B'}_{W}=\phi \left( \sum_{i=0}^{n-2}{ \sum_{j=i+1}^{n-1}{K[i][j]} } \right) - \sum_{i=0}^{n-2}{ \sum_{j=i+1}^{n-1}{\phi (K[i][j])} } \\ + \sum_{i=1}^{n-1}{ \sum_{j=0}^{i-1}{ \left( \phi (H(i,j))-\phi (K[i][j])-\phi (H(i,j)-K[i][j]) \right) } } \\ + \sum_{i=0}^{n-1}{\left( \phi (G(i)+K[i][i]) - \phi (G(i)) - \phi (K[i][i]) \right)},$$
$$\phi (x) = \frac{x \cdot \ln (x)-x+0.5 \cdot \ln (2 \cdot \pi \cdot x )}{\ln (2)}.$$
Затем выбирается наименьший по объему вариант кода с учетом необходимой для декодирования статистики в Омега-кодах Элиаса и сравнивается с суммарным весом дочерних узлов. Если объединение оказывается более выгодным, узел помечается как приоритетный и ему присваивается вес равный наименьшему объему кода, в противном случае ему присваивается суммарный вес дочерних узлов с учетом издержек на разграничение блоков. По завершению формирования всех узлов дерева, выполняется его обход сверху вниз слева направо и с учетом расставленных приоритетов выполняется итоговое разбиение данных на блоки.
Для большей компактности статистика подвергается ряду преобразований: упорядоченный алфавит преобразуется в дельта-код с вычетом единицы, а значения таблиц $F[n]$ и $FM[n]$ декрементируются. Преобразованная статистка может быть сохранена в виде последовательности Омега-кодов Элиаса или дополнительно сжата. Сжимать статистику предлагается рекурсивно комбинаторным методом без разбиения на блоки, до тех пор, пока это выгодно.
Балансировка по таким параметрам как скорость компрессии, степень сжатия и допустимые потери, играет важную роль при построении любого архиватора. Основные параметры архиватора измерительной информации, влияющие на степень сжатия и время кодирования, показаны на рисунке 5.
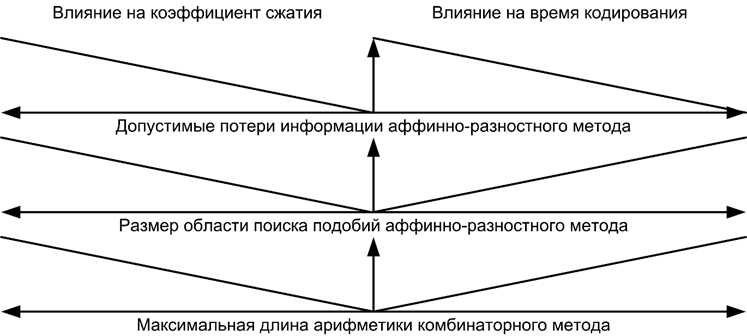
Рис. 5. Характер влияния параметров архиватора на время и коэффициент сжатия результатов измерений
В ходе исследований комбинаторного кодирования был проведен сравнительный анализ эффективности разработанного метода, метода Хаффмана и арифметического кодирования на большом объеме разнородных данных. В тестах был использован классическая реализация арифметического кодера [6] и реализация Хаффмана [7], которая была модифицирована для снятия ограничения на длину кодового слова.
Исследована зависимость времени кодирования и декодирования от длины арифметики, необходимой для сжатия последовательности данных комбинаторным методом (рис.6). С ростом длины арифметики симметрия комбинаторного кода нарушается в сторону меньшего времени декодирования, аналогичное явление наблюдается в коде Хаффмана, а арифметический код является практически симметричным.
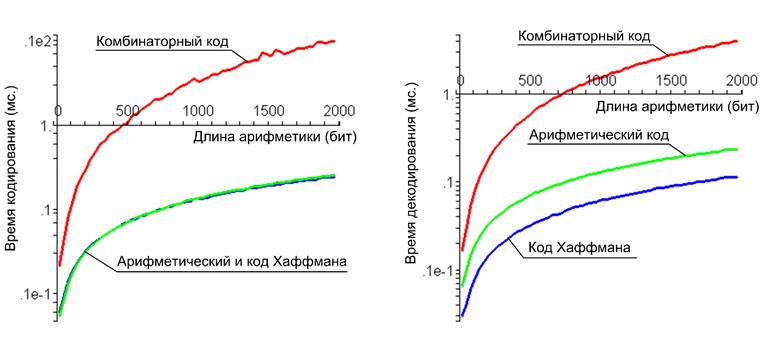
Рис. 6. Время работы алгоритмов относительно длины арифметики необходимой для комбинаторного кодирования
Эффективность рассматриваемых методов кодирования относительно энтропии нулевого порядка (рис.7) показывает, что на равных условиях комбинаторный метод позволяет получить более компактный код по сравнению с другими алгоритмами, пределом для которых является суммарная энтропия нулевого порядка. В расчетах эффективности кодирования учитывался только размер соответствующего кода без учета затрат на таблицу частот и алфавит. Даже если рассматривать универсальные адаптивные варианты арифметического кодирования и метода Хаффмана, то полученного преимущества вполне достаточно, чтобы компенсировать невозможность адаптивной реализации комбинаторного кодирования и сохранить превосходство в степени сжатия данных. Значительный всплеск в начале графика соответствующего методу Хаффмана связан с тем, что данный метод в отличии от арифметического не может кодировать символ менее чем одним битом. Среднее число бит на символ при использовании комбинаторного кодирования лишь в начале незначительно больше энтропии, это следствие того, что размер комбинаторного кода является целым значением. На рисунке 7 отсутствует график соответствующий серийному комбинаторному колу, поскольку он слабее связан с энтропией и сильно зависит от наличия монотонных последовательностей, при отсутствии которых он будет совпадать с простым комбинаторным кодом, а при их избытке будет приближаться к словарному комбинаторному коду.

Рис. 7. Эффективность статистических кодов относительно суммарной энтропии нулевого порядка
Время комбинаторного кодирования и декодирования быстро растет с увеличением самого кода, поэтому в случае кодирования значительных объемов данных потребовалось использовать блочную реализацию алгоритма, что все же не позволило обогнать классические методы и с точки зрения скорости они остаются предпочтительными. Кроме того, бесконечное увеличение размера комбинаторного кода не всегда приводило к лучшей степени сжатия, поэтому блочная реализация потребовалась не только для увеличения скорости, но и для степени сжатия. В таблице 1 приведены результаты работы алгоритмов статистического сжатия информации над файлами входящими в стандартную поставку Windows XP. Использовались следующие варианты алгоритмов сжатия:
- арифметический – универсальная адаптивная реализация;
- модифицированный Хаффмана – статистика сжата аналогично комбинаторному методу;
- комбинаторный – без ограничений на длину арифметики.
| Файл | Кодировщик | Время упаковки (мс.) | Время распаковки (мс.) | Коэффициент сжатия |
|---|---|---|---|---|
| Media\ringin.wav | Арифметический | 49 | 51 | 1.268 |
| 10026 байт | Хаффмана | 22 | 22 | 1.255 |
| Комбинаторный | 937 | 250 | 1.307 | |
| Кофейня.bmp | Арифметический | 85 | 82 | 1.441 |
| 17062 байт | Хаффмана | 28 | 33 | 1.431 |
| Комбинаторный | 2843 | 157 | 1.484 | |
| chkdsk.exe | Арифметический | 53 | 64 | 1.412 |
| 11776 байт | Хаффмана | 26 | 29 | 1.383 |
| Комбинаторный | 547 | 109 | 1.655 | |
| system32\eula.txt | Арифметический | 69 | 69 | 1.466 |
| 33489 байт | Хаффмана | 44 | 60 | 1.457 |
| Комбинаторный | 93071 | 4842 | 1.878 |
Зависимость времени кодирования и коэффициента сжатия от максимально допустимой длины арифметики продемонстрирована на рисунке 8, в качестве кодируемой информации использовался первый файл таблицы 1. Полученная зависимость по своему характеру полностью соответствует предсказанному поведению алгоритма (рис.5).
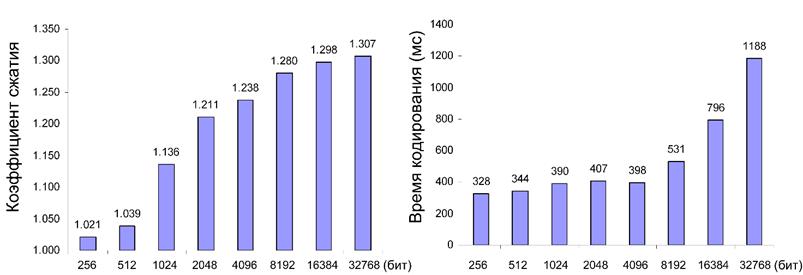
Рис. 8. Влияние ограничения длины арифметики на время и степень сжатия данных
Асимметрия комбинаторного кодирования может достигать нескольких порядков в сторону уменьшения времени декодирования. Существенно сократить время кодирования и декодирования позволяет использование таблиц предварительно рассчитанных биномиальных коэффициентов. Для выполнения операций длинной арифметики при комбинаторном кодировании применялась открытая библиотека GNU MP [8].
Библиографический список
- Новиков Ф.А. Дискретная математика для программистов: учебник для вузов. 3-е изд. – СПб.: Питер, 2009. – 384 с.
- Устян А.Е. Алгебра и теория чисел: В 2 ч. Учебное пособие. Ч.1 / 2-е изд., доп. и перераб. – Тула: Изд-во гос. пед. ун-та, 2002. – 236 с.
- Intel® 64 and IA-32 Architectures Software Developer’s Manual – Vol. 1. – Order Number: 253665-034US. – March 2010 [Electronic resource]. URL: http://www.intel.com/Assets/PDF/manual/253665.pdf (access date 09.07.2010).
- Симаков А. Код Хаффмана // Сыктывкарский Государственный Университет, Кафедра Прикладной Математики. – Октябрь 2002 [Электронный ресурс]. URL: http://www.compression.ru (дата обращения 09.07.2010).
- Pearson, Karl. Historical note on the origin of the normal curve of errors. // Biometrika Т. 16. – pp. 402–404.
- Nelson M. Arithmetic Coding + Statistical Modeling = Data Compression. – 1991 [Electronic resource]. URL: http://www.dogma.net/markn/articles/arith/part1.htm (access date 09.07.2010).
- Static Huffman compression/decompression by William Demas – 14 August 1990. – Version 1.0 [Electronic resource]. URL: http://www.maxime.net.ru/lds (access date 09.07.2010).
- GNU MP Manual. / Free Software Foundation, Inc. 2008. [Electronic resource]. URL: http://gmplib.org/
 Проект эмуляции
Проект эмуляции